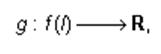Derivadas: primeros teoremas de aplicacion

DERIVADAS: PRIMEROS TEOREMAS

Derivada de una función constante

 

Sea una función constante f(x) = C.

Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que para cualquier valor de la abscisa su ordenada correspondiente es, constantemente, igual a C, si a es un punto cualquiera del campo de definición de f(x),

 

                            f(a + h) - f(a) = C - C = 0, por lo que

 

                      

 

 

 

Luego la derivada de una constante es siempre cero.

 

                                      

Derivadas de las funciones exponenciales a^x y e^x

 

Sea la función y = a^x, siendo a una constante positiva distinta de 1. La derivada de esta función en un punto x es:

 

                                                y se toman logaritmos neperianos:

 

                         

Derivada de una raiz

La derivada de la raíz enésima de una función es igual a la derivada del radicando partida por la n veces la raíz enésima de la función radicando elevada a n menos uno.

Derivada de la raíz cuadrada

La derivada de la raíz cuadrada de una función es igual a la derivada del radicando partida por el duplo de la raíz.

Derivada de un producto de funciones

 

Sean f y g dos funciones definidas y derivables en un mismo punto x.

 

            

 Si se suma y se resta en el numerador f(x) · g(x + h), la fracción anterior no varía,

 

          

 Sacando g(x + h) factor común en los dos primeros sumandos, y f(x) en los otros dos,

 

                 

                           

 

Regla de  la cadena

 

Esta propiedad asegura que si y = f(x) es una función derivable en un cierto intervalo I,

 

                                            

 

y z = g(y) es otra función derivable y definida en otro intervalo que contiene a todos los valores (imágenes) de la función f,

 

                                         

 

entonces la función compuesta

 

                                     

 

definida por (g o f) (x) = g[f(x)], es derivable en todo punto x de I y se obtiene

 

                               

Funciones implícitas

Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.

Derivadas de funciones implícitas

Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:

x'=1.

En general y'≠1.

Por lo que omitiremos x' y dejaremos y'.

Cuando las funciones son más complejas vamos a utilizar una regla para facilitar el cálculo:

 

 

Bibliografia: http://www.sectormatematica.cl/contenidos/cadena.htm

MALLA

MALLA DEL CURSO

OBJETIVO DE GRADO:

Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA:

¿cuáles deben ser las dimensiones óptimas para que el costo del material empleado en una lata de cerveza,coca-cola o atú´sea mínima?

CONCLUSIONES.

• La malla es una guia para que los estudiantes esten enterados sobre como y que se va a trabajar.
• Estudiar algunas temas de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo. estos temas seran de gran utilidadd en el futuro, y tambien se pretende que los estudiantes se familiarican un poco mas con el tema.
• Con la pregunta problematizadora dada en cada periodo se pretende dar a conocer el tema que se va a tratar y si los estudiantes lo  desean pueden ir consultando el tema por adelantado, lo cual crea una conciencia de autoayuda y autonomia en los alumnos. 

 

GRADO:        ONCE PERIODO:    PRIMERO

INTENSIDAD HORARIA :   3 horas semanales DOCENTE:                           GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

Desigualdades e Inecuaciones. Axiomas de orden en R. Intervalos. Propiedades de las desigualdades Problemas. VALOR ABSOLUTO. Definición. Propiedades. Ejercicios FUNCIONES. Definición. Funciones básicas Dominio, Rango Problemas de la vida.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Resolver inecuaciones por  el método del cementerio Y el método analítico. Resolver ecuaciones e inecuación que contienen valores absolutos. Aplicar la definición de función a diferentes relaciones. Resolver problemas que involucran funciones.

Resuelve inecuaciones por  el método del cementerio Y el método analítico. Resuelve ecuaciones e inecuación que contienen valores absolutos. Aplica la definición de función a diferentes Resuelve problemas que involucran funciones.

1. La solución de inecuaciones por  el método del cementerio Y el método analítico. 2. La solución de   ecuaciones e inecuación que contienen valores absolutos. 3.  La aplicación de  la definición de función a diferentes relaciones 4. La solución a problemas que involucran funciones. El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

GRADO:        ONCE PERIODO:     SEGUNDO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

Transformación de funciones. Desplazamientos Verticales. Desplazamiento horizontal. Reflexión. Estiramiento y acortamiento vertical. Acortamiento y alargamiento horizontal. Función par e impar. Dominio, Rango. Interceptos. Función uno a uno Y sobre. Función Inyectiva. Función Inversa.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Graficar funciones partiendo de funciones básicas, empleando los conceptos de traslación, estiramiento, encogimiento y reflexión. Determinar el Dominio, el Rango y los intersectos de una función. Identificar, clasificar una función en par o impar. Identificar si una función tiene inversa y calcularla.

Grafica funciones partiendo de funciones básicas, empleando los conceptos de traslación, estiramiento, encogimiento y reflexión. Determina el Dominio, el Rango y los intersectos de una función. Identifica, clasifica una función en par o impar. Identifica si una función tiene inversa y la calcula

1. La gráfica de una función usando funciones básicas, desplazamientos verticales y horizontales. 2. La gráfica de una función usando funciones básicas, alargamientos y reflexiones verticales y horizontales 3. El cálculo del Dominio, Rango, Interceptos. 4. La determinación si la gráfica de una FUNCIÓN es inyectiva y, si por lo tanto tiene Inversa. . El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.

GRADO:        ONCE PERIODO:     TERCERO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

LIMITES. Definición, ejemplos, ejercicios Continuidad, Teorema del valor intermedio. DERIVADA. Recta tangente y normal a una curva. Velocidad instantánea. Definición de Derivada. Reglas de derivación. Regla de la cadena Derivada implícita.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Calcular límites cuando la variable tiende a un valor finito. Eliminar indeterminaciones de la forma 0/0. Determinar la continuidad de una función. Calcular la derivada de funciones.

Calcula límites cuando la variable tiende a un valor finito. Elimina indeterminaciones de la forma 0/0. Determina la continuidad de una función. Calcula la derivada de funciones.

1. El cálculo de límites cuando la variable tiende a un valor finito. 2. La eliminación de indeterminaciones de la forma 0/0. 3. La determinación de la continuidad o no de una función. 4. El calcular la derivada de una función real. . El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.

GRADO:        ONCE PERIODO:     CUARTO

INTENSIDAD HORARIA :    3 horas semanales DOCENTE:                            GUILLERMO LEÓN ROLDÁN SOSA

OBJETIVO DE GRADO: Estudiar funciones de variable real, límites y  derivadas, como conceptos básicos para resolver problemas de la vida, que involucren minimizar o maximizar cantidades, costos, áreas, tiempo.

PREGUNTA PROBLEMATIZADORA: ¿CUÁLES DEBEN SER LAS DIMENSIONES ÓPTIMAS PARA QUE EL COSTO DEL MATERIAL EMPLEADO EN UNA LATA DE CERVEZA, COCACOLA O ATÚN SEA MINIMO?

CONTENIDOS

ESTANDARES

COMPETENCIAS

LOGROS

INDICADORES DE DESEMPEÑO

INSTANCIAS VERIFICADORAS

ACCIONES EVALUATIVAS

FECHAS

APLICACIONES DE LA DERIVADA. Máximos y mínimos relativos y absolutos. Números críticos. Teorema del valor medio y el valor extremo. Criterios de la primera y segunda derivada Concavidad. Problemas de OPTIMIZACIÖN.

Pensamiento numérico y sistemas numéricos Pensamiento variacional   y sistemas algebraicos y analíticos

Formular, plantear, transformar y resolver problemas a partir de situaciones de la vida cotidiana, de las otras ciencias y de las matemáticas mismas. Utilizar diferentes registros de representación o sistemas de notación simbólica para crear, expresar y representar ideas matemáticas; para utilizar y transformar dichas representaciones y, con ellas, formular y sustentar puntos de vista Usar la argumentación, la prueba y la refutación, el ejemplo y el contraejemplo, como medios de validar y rechazar conjeturas, y avanzar en el camino hacia la demostración. Dominar procedimientos y algoritmos matemáticos y conocer cómo, cuándo y porqué usarlos de manera  flexible y eficaz.

Hallar máximos y mínimos relativos y absolutos de una función. Obtener valores críticos de una función. Determinar intervalos de crecimiento y decrecimiento. Determinar concavidad. Resolver problemas de Optimización

Halla máximos y mínimos relativos y absolutos de una función. Obtiene valores críticos de una función. Determina intervalos de crecimiento y decrecimiento. Determina concavidad. Resuelve problemas de Optimización

1. Los máximos y mínimos relativos y absolutos de una función. 2. Los valores críticos de una función. 3. Los intervalos de crecimiento y decrecimiento. La Determinación de la concavidad. 4. La solución de problemas de Optimización El valor y el respeto al trabajo y la participación del otro, en todos los ámbitos académicos y de convivencia.

Evaluación escrita Evaluación escrita Evaluación escrita Evaluación escrita .

Semana 4 Semana 5 Semana 6 Semana 8

RECURSOS PEDAGOGICOS Ordenadores, programas o proyectos virtuales como DESCARTES y GEOGEBRA, DVD’, sala de informática, Internet, libros virtuales, papel cuadriculado, lápiz, reglas, escuadras, libros , fotocopias, borradores, tizas, marcadores, GRUPO GALOIS.